力扣刷题日常(1-2)

第一题: 两数之和(难度: 简单)

原题:

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那 两个 整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案，并且你不能使用两次相同的元素。

你可以按任意顺序返回答案。

示例 1：

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

示例 2：

输入：nums = [3,2,4], target = 6
输出：[1,2]

示例 3：

输入：nums = [3,3], target = 6
输出：[0,1]

提示：

• 2 <= nums.length <= 104
• -109 <= nums[i] <= 109
• -109 <= target <= 109
• 只会存在一个有效答案

**进阶：**你可以想出一个时间复杂度小于 O(n2) 的算法吗？

---

官方提示(附翻译)

1. A really brute force way would be to search for all possible pairs of numbers but that would be too slow. Again, it’s best to try out brute force solutions for just for completeness. It is from these brute force solutions that you can come up with optimizations.(一种非常暴力的方法是搜索所有可能的数字对，但这会太慢。同样，为了完整性，最好尝试一下暴力解决方案。正是从这些暴力解决方案中，你才能想出优化方法。)

2. So, if we fix one of the numbers, say x, we have to scan the entire array to find the next number y which is value - x where value is the input parameter. Can we change our array somehow so that this search becomes faster?(所以，如果我们固定其中一个数字，比如说 x ，我们就得扫描整个数组来寻找下一个数字 y ，它等于 value - x ，其中 value 是输入参数。我们能否以某种方式改变我们的数组，从而使这种搜索变得更快？)

3. The second train of thought is, without changing the array, can we use additional space somehow? Like maybe a hash map to speed up the search?(第二种思路是，在不改变数组的情况下，我们能否以某种方式使用额外的空间？比如，或许可以使用哈希表来加快搜索速度？)

---

开始解题:

思路一: 暴力解题

老实说在第一眼看到这个题的时候,我也是有点懵的,因为这和我在其他平台见过的两数之和完全不同,不过没关系,我们完全可以先暴力解题.那对于这道题来说,暴力解题的方法显而易见,两个 for 循环,当然各位也可能直接就有了自己的想法,我这里只阐述我自己的看法.

那么它的流程就应该像下面这样

1. 选择第一个数: 我们从数组的第一个元素开始,用一个大循环(也可以叫做外层循环)来依次选择第一个数,比如 nums[i].
2. 选择第二个数: 对于每一个选定的 nums[i] ,我们都需要在数组的剩余部分寻找一个数 nums[j] ,看看它们俩的和是不是 target .所以,我们在大循环的内部再嵌套一个小循环(内层循环), 从 i+1 的位置开始遍历(因为我们找的是和,所以是一个组合问题,不是排列问题),这样我们不会重复使用同一个元素
3. 判断和: 在小循环中,我们检查 nums[i] + nums[j] 是否等于 target .
   • 如果相等,则可以直接直接输出它们的下标 [i,j].
   • 如果不相等，则内圈循环继续，知道所有的可能性检查完。

复杂度分析:

• 时间复杂度: O(n²)。因为我们用了两层嵌套循环，在最坏的情况下，外层循环执行n次，内层循环平均执行n/2次，总的计算量与 n * n 成正比。
• 空间复杂度: O(1)。我们没有使用额外的、随数组大小变化的存储空间。

思路总结: 这个方法虽然简单，但当数组非常大时，n² 的计算量会变得非常缓慢。题目的“进阶”提示也暗示我们，有比 O(n²) 更好的方法。

---

思路二: 哈希表优化

那么这类问题的标准是什么呢.核心思想就是用空间换时间.

我们上面讲的暴力解法的瓶颈在于“寻找”第二个数的过程太慢了。对于每个 nums[i]，我们都要遍历一遍数组的剩余部分来寻找 target - nums[i]。如果能让这个“寻找”过程变得飞快，问题就解决了。

那什么数据结构查找起来最快呢？哈希表（在C#中是 Dictionary，在C++中是 unordered_map）。它能提供平均 O(1) 时间复杂度的查找、插入和删除操作。

那么我们的实现逻辑应该是这样的

1. 创建哈希表：我们创建一个哈希表，用来存储我们“遍历过”的数字及其对应的下标。键（Key）是数组中的值，值（Value）是该值对应的下标。
2. 单次遍历：我们只需要遍历一次数组。对于数组中的每一个元素 nums[i]：
   a. 计算补数：计算出我们需要的“另一半”：complement = target - nums[i]。
   b. 查找哈希表：现在，我们不去数组里傻傻地找 complement 了，而是去哈希表里查一下，看看 complement 这个键（Key）是否存在。
   • 如果存在：这说明 complement 这个数字我们之前已经遇到过了。我们直接从哈希表中取出它的下标，再配上当前元素的下标 i，就是最终答案。
   • 如果不存在：说明到目前为止，我们还没遇到能和 nums[i] 配对的数字。那么，nums[i] 本身可能就是未来某个数字的“另一半”。所以，我们把当前数字 nums[i] 和它的下标 i 存入哈希表中，以备后续的元素查询。

这里我们举个栗子: nums = [2, 7, 11, 15], target = 9

• 初始化：创建一个空的哈希表 map。
• 循环 i = 0，当前元素 nums[0] (值为 2)。
  • 计算补数：complement = 9 - 2 = 7。
  • 查哈希表：map 中有键 7 吗？没有，map 是空的。
  • 将当前元素存入哈希表：map.Add(2, 0)。现在 map 是 {2: 0}。
• 循环 i = 1，当前元素 nums[1] (值为 7)。
  • 计算补数：complement = 9 - 7 = 2。
  • 查哈希表：map 中有键 2 吗？有！ 它的值（下标）是 0。
  • 我们找到了,返回 map 中 2 的下标 0 和当前下标 1。最终结果 [0, 1]。

复杂度分析:

• 时间复杂度: O(n)。我们只遍历了数组一次。哈希表的插入和查找操作平均都是 O(1)。
• 空间复杂度: O(n)。在最坏的情况下，我们可能需要将数组中所有元素都存入哈希表。

思路总结: 这个方法用一个哈希表的额外空间，将时间复杂度从 O(n²) 成功降到了 O(n)，是这道题的最优解。

---

解法语句(仅方法二):

public class Solution {
    public int[] TwoSum(int[] nums, int target) {

        Dictionary<int, int> map = new Dictionary<int, int>();

        for (int i = 0; i < nums.Length; i++) {
            int currentNum = nums[i];
            int complement = target - currentNum;

            if (map.ContainsKey(complement)) {
                return new int[] { map[complement], i };
            }
            map[currentNum] = i;
        }

        return new int[0]; 
    }
}

这里最主要的方法是**map.ContainsKey(complement)**

• 这是一个非常重要且常用的方法，用于检查字典中是否包含指定的键（Key）。它返回一个布尔值（true 或 false），并且这个操作的平均时间复杂度是 O(1)，非常高效。

---

知识点总结与举一反三(待补充)

---

第二题: 两数相加(难度: 中等)

原题:

给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。

请你将两个数相加，并以相同形式返回一个表示和的链表。

你可以假设除了数字 0 之外，这两个数都不会以 0 开头。

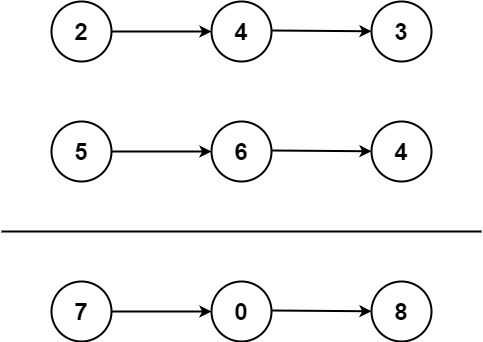
示例 1：

输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[7,0,8]
解释：342 + 465 = 807.

示例 2：

输入：l1 = [0], l2 = [0]
输出：[0]

示例 3：

输入：l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出：[8,9,9,9,0,0,0,1]

提示：

• 每个链表中的节点数在范围 [1, 100] 内
• 0 <= Node.val <= 9
• 题目数据保证列表表示的数字不含前导零

---

开始解题:

那我作为 Unity 工程师呢,我可以把这个问题进行一个比喻.就比如我们现在有几条路(链表),路上插着几个独立的路标(节点),每个路标上只有一个数字,并且指向下一块路标,我们现在的任务就是沿着两条这样的路径，把每个对应路标上的数字加起来，形成一条新的路径。

算法逻辑详解:

其实这道题的思路和我们小学学过的列竖式加法的过程类似.

以 342 + 465 为例,我们从个位开始加. 2+5=7.然后是十位 4+6=10,我们写下0,然后往百位进一位.最后是百位, 3+4,再加上刚才进上来的1,最后等于8.最后结果为807.

那么这道题目给我们创造了这一个环境,数字是 逆序 存储的.也就是说,链表的第一个节点,就是数字的 个位.

• l1 = [2,4,3] 代表 342
• l2 = [5,6,4] 代表 465

链表的头节点 l1.val=2 和 l2.val=5 正好就是个位数

那么我们的算法步骤就可以进行分解了

1. 初始化:

   • 我们需要一个变量 carry 来存储“进位”，初始时没有进位，所以 carry = 0。
   • 我们需要一条新的链表来存放结果。为了方便操作，我们通常会创建一个“虚拟头节点”（dummy head）。这就像在拼乐高前，先放一个临时的底座，最后拼好了再把这个底座拿掉。我们用一个指针 current 指向这个虚拟头节点，之后每产生一个新节点，就接在 current 后面。

2. 遍历与计算:

   • 我们从两个链表的头节点开始，同步向后遍历。

   • 在每一步，我们都取出两个链表当前节点的值。如果其中一个链表已经遍历完了（比如 l1 比 l2 短），我们就认为它的当前值是 0。

   • 计算总和：sum = l1当前节点值 + l2当前节点值 + carry。

     • 根据 sum 计算出要存入新节点的值和新的进位：
       • 新节点的值应该是 sum % 10 （% 是取余数，比如 17 % 10 结果是 7）。
       • 新的进位 carry 应该是 sum / 10 （在C#中，两个整数相除会自动舍去小数，比如 17 / 10 结果是 1）。

   • 创建这个新节点，并将其链接到结果链表的末尾。然后，current 指针也向后移动到这个新节点上，为下一次链接做准备。

3. 循环终止条件: 只要两个链表中还有一个没有遍历完，或者 carry 不为0（处理最高位的进位，例如 99+1=100），我们的循环就要继续。

4. 返回结果: 循环结束后，我们想要的完整结果链表就是我们创建的“虚拟头节点”的下一个节点。

我们简单举一个栗子吧:

l1 = [2,4,3], l2 = [5,6,4]

• 第1步 (个位):
  • carry = 0
  • sum = 2 + 5 + 0 = 7
  • 新节点值为 7 % 10 = 7，新 carry = 7 / 10 = 0。
  • 结果链表: [7]
• 第2步 (十位):
  • carry = 0
  • sum = 4 + 6 + 0 = 10
  • 新节点值为 10 % 10 = 0，新 carry = 10 / 10 = 1。
  • 结果链表: [7, 0]
• 第3步 (百位):
  • carry = 1
  • sum = 3 + 4 + 1 = 8
  • 新节点值为 8 % 10 = 8，新 carry = 8 / 10 = 0。
  • 结果链表: [7, 0, 8]
• 结束:
  • l1 和 l2 都遍历完了，carry 也变回了 0。循环结束。返回结果 [7, 0, 8]。

---

解法语句:

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     public int val;
 *     public ListNode next;
 *     public ListNode(int val=0, ListNode next=null) {
 *         this.val = val;
 *         this.next = next;
 *     }
 * }
 */
public class Solution {
    public ListNode AddTwoNumbers(ListNode l1, ListNode l2) {
        // 1. 初始化：创建一个虚拟头节点，方便我们操作链表
        ListNode dummyHead = new ListNode(0); 
        // 创建一个“当前”指针，用于构建新的结果链表
        ListNode current = dummyHead; 
        // 初始化进位值为0
        int carry = 0; 

        // 2. 循环：只要l1或l2不为空，或者还有进位，就继续计算
        while (l1 != null || l2 != null || carry != 0) {
            // 获取l1和l2的当前节点值，如果节点为空，则值为0
            int v1 = (l1 != null) ? l1.val : 0;
            int v2 = (l2 != null) ? l2.val : 0;

            // 计算总和 = 节点1的值 + 节点2的值 + 上一步的进位
            int sum = v1 + v2 + carry;

            // 更新进位值，为下一次循环做准备
            carry = sum / 10;
            
            // 创建新节点，值为总和的个位数
            // 并将其链接到结果链表的末尾
            current.next = new ListNode(sum % 10);
            
            // 将“当前”指针移动到新创建的节点上
            current = current.next;

            // 将l1和l2指针向后移动（如果它们不为空）
            if (l1 != null) {
                l1 = l1.next;
            }
            if (l2 != null) {
                l2 = l2.next;
            }
        }

        // 3. 返回结果：虚拟头节点的下一个节点才是我们真正结果链表的头
        return dummyHead.next;
    }
}

代码讲解:

1. 那么上面的代码用到了一个特殊的用法

int v1 = (l1 != null) ? l1.val : 0; - 三元运算符

• 这是一个非常简洁的 if-else 写法，称为三元运算符。
• 它的结构是 condition ? value_if_true : value_if_false。
• 这行代码等价于：

int v1;
if (l1 != null) {
    v1 = l1.val;
} else {
    v1 = 0;
}

2. 对 dummyHead 和最后的 return dummyHead.next 的讲解:

dummyHead 有一个名字----虚拟头节点/哨兵节点,是一个非常经典且有用的技巧.

我们先来一个简单的比喻吧----穿珠子

想象一下，我们要用线把一堆珠子（ListNode）串成一条手链（结果链表）。

• 没有 dummyHead 的情况：

  1. 我们拿起第一个珠子。因为是第一个，我们的两只手都很忙，一只手要捏住珠子，另一只手要拿线准备穿过去。这个动作很特别。
  2. 然后，我们拿起第二个珠子。现在我们一只手捏着已经穿好的第一个珠子和线头，另一只手拿新珠子穿进去。这个动作和第一步不一样。
  3. 之后所有珠子，都重复第二步的动作。

  我们看，处理第一个珠子的方式和处理后续所有珠子的方式是不同的。在代码里，这就意味着你需要在循环里写一个 if 判断，来专门处理“头节点为空”的特殊情况。

• 有 dummyHead 的情况：

  1. 我们不是直接开始穿珠子，而是先在线的末端系上一个临时的、不起眼的小疙瘩（这就是 dummyHead）。这个小疙瘩你最后会剪掉。
  2. 现在，我们拿起第一个“真正”的珠子，把它穿在线上，挨着那个小疙瘩。
  3. 我们拿起第二个“真正”的珠子，把它穿在线上，挨着第一个珠子。
  4. 我们拿起第 N 个“真正”的珠子，把它穿在线上，挨着第 N-1 个珠子。

  发现了么？有了这个“小疙瘩”作为起点，我们每一次穿珠子的动作都变得完全一样了！你不需要再特殊处理第一个珠子。

这个比喻可能还是有些难以理解,没关系,我们回到代码里看看

• 为什么需要 dummyHead？——为了简化操作

我们的目标是创建一个新链表。在循环的每一步，我们都会创建一个新节点 newNode。

如果没有 dummyHead，代码会长这样：

public ListNode AddTwoNumbers(ListNode l1, ListNode l2) {
    ListNode resultHead = null; // 结果链表的头，一开始是空的
    ListNode current = null;    // 当前节点指针
    int carry = 0;

    while (l1 != null || l2 != null || carry != 0) {
        // sum, carry 的逻辑不变
        int sum = ...;
        carry = sum / 10;
      
        ListNode newNode = new ListNode(sum % 10);

        // 这里是关键的、繁琐的部分
        if (resultHead == null) {
            // 如果是第一个节点
            resultHead = newNode;
            current = newNode;
        } else {
            // 如果不是第一个节点
            current.next = newNode;
            current = current.next;
        }
      
        //移动 l1, l2 的逻辑不变
    }
    return resultHead;
}

看到 if-else 了吗？它必须在每一次循环中都进行判断，这既不优雅，也稍微增加了一点点计算开销。

有了 dummyHead，代码就变得统一和简洁：

ListNode dummyHead = new ListNode(0); // 创建“小疙瘩”
ListNode current = dummyHead;         // 用手先捏住这个“小疙瘩”

while (l1 != null || l2 != null || carry != 0) {
    // 计算逻辑不变
  
    // 每次的动作都完全一样：
    // 把新珠子(newNode)接到手捏着的那个珠子(current)后面
    current.next = new ListNode(sum % 10); 
    // 然后手向前移动，捏住刚穿好的新珠子
    current = current.next; 
}

dummyHead 的存在，确保了 current 指针一开始就指向一个实际的对象，而不是 null。因此，current.next = ... 这个操作永远不会因为 current 是 null 而报错。我们成功地消除了对第一个节点的特殊处理。

• 为什么是 return dummyHead.next？——因为“小疙瘩”不是我们要的结果

循环结束后，我们的链表结构是这样的（以 [7,0,8] 为例)：

• dummyHead 这个变量，从始至终都指向我们最开始创建的那个值为 0 的临时节点。它就像那个我们不打算送人的“小疙瘩”。
• 我们真正想要的手链（结果链表），是从第一个有意义的珠子，也就是值为 7 的那个节点开始的。
• 这个值为 7 的节点，正好是 dummyHead 节点的 next 指针所指向的地方。

所以，return dummyHead.next; 的意思就是：“好了，手链穿完了，现在我们把开头的那个临时小疙瘩忽略掉，把从第一个真正的珠子开始的整条链返回给别人。”

总结一下：

• dummyHead 是一个编程技巧，它是一个辅助性的、不属于最终结果的节点。它的核心作用是简化链表头部的插入操作，让循环逻辑保持统一，避免对空链表进行特殊判断。
• return dummyHead.next 是因为 dummyHead 本身是我们的“脚手架”，而真正的“建筑”（结果链表）是从它的下一个节点开始的。返回 dummyHead.next 就是返回我们真正构建的结果。